10 Class Mathematics All Exercises Notes

Here we will provide you with the 10 class mathematics all exercises notes.

• Define quadratic equation.
• Solve a quadratic equation in one variable by factorization.
• Solve a quadratic equation in one variable by completing the square.
• Derive quadratic formula by using the method of completing the square.
• Solve a quadratic equation by using the quadratic formula.
• Solve the equations of the type ax⁴ + bx² + c = 0 by reducing it to the quadratic form.
• Solve the equations of the type a p(x) + =
• Solve reciprocal equations of the type a (x² + )+ b (x +   ) + c = 0
• Solve exponential equations involving variables in exponents.
• Solve equations of the type (x + a) (x + b) (x + c) (x + d) = k
• Where a + b = c + d.
• Solve radical equations of the types
  1. √ax + b = cx + d,
  2. √√x+a+√√x+b = √√x+c,
  3. √√x² + px + m + √√x² + px + n = q.
• Exercise 1.1
• Exercise 1.2
• Exercise 1.3
• Exercise 1.4
• Miscellaneous Exercise

• Define discriminant (b² – 4ac) of the quadratic expression ax² +bx+c.
• Find the discriminant of a given quadratic equation.
• Discuss the nature of roots of a quadratic equation through discriminant.
• Determine the nature of the roots of a given quadratic equation and verify the result by solving the equation.
• Determine the value of an unknown involved in a given quadratic
• Equation when the nature of its roots is given.
• Find cube roots of unity.
• Recognize complex cube roots of unity as w and w?
• Prove the properties of cube roots of unity.
• Use properties of cube roots of unity to solve appropriate problems.
• Find the relation between a quadratic equation’s roots and coefficients.
• Find the sum and product of roots of a given quadratic equation without solving it.
• Find the value(s) of unknown(s) involved in a given quadratic equation

When

• Sum of roots is equal to a multiple of the product of roots,
• Sum of the squares of roots is equal to a given number,
• Roots differ by a given number,
• Roots satisfy a given relation (e.g., the relation 2 α +50= 7 where α and bare the roots of the given equation),
• Both sum and product of roots are equal to a given number.
• Define symmetric functions of roots of a quadratic equation.
• Evaluate a symmetric function of the roots of a quadratic equation in terms of its coefficients.
• Establish the formula, X²-(sum of roots) x + (product of roots) = 0, to find a quadratic equation from the given roots.
• Form the quadratic equation whose roots, for example, are of the type:

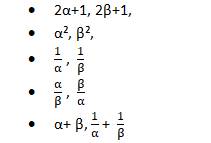
Where α  and β are the roots of a given quadratic equation.

• Describe the method of synthetic division.
• Use synthetic division to
• Find the  quotient and remainder when a given polynomial is divided by a linear polynomial,
• Find the value(s) of unknown(s) if the zeros of a polynomial are given,
• Find the value(s) of unknown(s) if the factors of a polynomial are given,
• Solve a cubic equation if one root of the equation is given,
• Solve a biquadratic (quartic) equation if two of the real roots of the equation are given.
• Solve a system of two equations in two variables when
• One equation is linear and the other is quadratic,
• Both equations are quadratic.
• Solve real-life problems leading to quadratic equations.

• Exercise 2.1
• Exercise 2.2
• Exercise 2.3
• Exercise 2.4
• Exercise 2.5
• Exercise 2.6
• Exercise 2.7
• Exercise 2.8
• Miscellaneous Exercise

• Define ratio, proportions and variations (direct and inverse).
• Find 3rd, 4th, mean and continued proportion.
• Apply theorems of invertendo, alternendo, componendo, dividendo and
• Componendo & dividendo to find proportions.
• Define joint variation.
• Solve problems related to joint variation.
• Use the method to prove conditional equalities involving proportions.
• Solve real-life problems based on variations.
• Exercise 3.1
• Exercise 3.2
• Exercise 3.3
• Exercise 3.4
• Exercise 3.5
• Exercise 3.6
• Exercise 3.7
• Chapter 3 MCQ’s
• Miscellaneous Exercise

• Define proper, improper and rational fractions.
• A resolve an algebraic fraction into partial fractions when its denominator

Consists of

• Non-repeated linear factors,
• Repeated linear factors,
• Non-repeated quadratic factors,
• Repeated quadratic factors.
• Exercise 4.1
• Exercise 4.2
• Exercise 4.3
• Exercise 4.4
• Chapter 4 MCQ’s
• Miscellaneous Exercise

• Sets
  Recall the sets denoted by n, w, z, e, o, p and q.
  Recognize operation on sets (u,∩, \, …)
  Perform operations on sets union, intersection, difference, complement.
  Give formal proofs of the following fundamental properties of union and intersection of two or three sets.
  Commutative property of union,
  Commutative property of intersection,
  Associative property of union,
  Associative property of intersection,
  Distributive property of union over intersection,
  Distributive property of intersection over union,
  De Morgan’s laws.
  Verify the fundamental properties for given sets.
  Use Venn diagram to represent
  Union and intersection of sets,
  Complement of a set.
  Use Venn diagram to verify
  Commutative law for union and intersection of sets,
  De Morgan’s laws,
  Associative laws,
  Distributive laws.
  Recognize ordered pairs and cartesian product.
  Define binary relation and identify its domain and range.
  Define function and identify its domain, co-domain and range.
  Demonstrate the following
  Into function,
  One-one function,
  Into and one-one function (injective function),
  Onto function (surjective function),
  One-one and onto function (bijective function).
  Examine whether a given relation is a function or not.
  Differentiate between one-one correspondence and one-one function.
  Include sufficient exercises to classify/differentiate between the above concepts.
• Exercise 5.1 
• Exercise 5.2
• Exercise 5.3
• Exercise 5.4
• Exercise 5.5
• Chapter 5 MCQ’s
• Miscellaneous Exercise

• Construct grouped frequency table.
• Construct histograms with equal and unequal class intervals.
• Construct a frequency polygon.
• Construct a cumulative frequency table.
• Draw a cumulative frequency polygon.
• Calculate (for ungrouped and grouped data)
  • Arithmetic mean by definition and using deviations from assumed mean.
• Calculate median, mode, geometric mean, harmonic mean.
• Recognize properties of the arithmetic mean.
• Calculate weighted mean and moving averages.
• Estimate median, quartiles and mode graphically.
• Measure range, variance and standard deviation.
• Exercise 6.1
• Exercise 6.2
• Exercise 6.3
• Chapter 6 MCQ’s 
• Miscellaneous Exercise

• Measure an angle in degree, minutes and seconds.
• Convert an angle given in degrees, minutes and seconds into decimal form and vice versa.
• Define a radian (a measure of an angle in n circular system) and prove the relationship between radians and degrees.
• Establish the rule 1 = rθ, where r is the radius of the circle, I the length of
• Circular arc and the central angle measured in radians.
• Prove that the area of a sector of a circle is 1/2r²θ.
• Define and identify:
  • General angle (conterminal angles),
  • Angle in standard position.
• Recognize quadrants and quadrantal angles.
• Define trigonometric ratios and their reciprocals with the help of a unit circle.
• Recall the values of trigonometric ratios for 45°, 30°, and 60°.
• Recognize signs of trigonometric ratios in different quadrants.
• Find values of remaining trigonometric ratios if one trigonometric ratio is given.
• Calculate the values of trigonometric ratios for 0°, 90°, 180°, 270°, 360°.
• Prove the trigonometric identities and apply them to show different trigonometric relations.
• Find the angle of elevation and depression.
• Soreal-lifelife problems involving angle of elevation and depression.
• Exercise 7.1
• Exercise 7.2
• Exercise 7.3
• Exercise 7.4
• Exercise 7.5
• Chapter 7 MCQ’s
• Miscellaneous Exercise

Prove the following theorems along with corollaries and apply them to solve appropriate problems.

• In an obtuse-angled triangle, the square on the side opposite to the obtuse angle is equal to the sum of the squares on the sides containing the obtuse angle together with twice the rectangle contained by one of the sides, and the projection on it of the other.
• In any triangle, the square on the side opposite to an acute angle is equal to the sum of the squares on the sides containing that acute angle diminished by twice the rectangle contained by one of those sides and the projection on it of the other.
• In any triangle, the sum of the squares on any two sides is equal to twice the square on half the third side together with twice the square on the median which bisects the third side (Apollonius’ Theorem).
• Exercise 8.1
• Exercise 8.2
• Miscellaneous Exercise

Prove the following theorems along with corollaries and apply them to solve appropriate problems.

• One and only one circle can pass through three non-collinear points.
• A straight line, drawn from the centre of a circle to bisect a chord (which is not a diameter) is perpendicular to the chord.
• Perpendicular from the centre of a circle on a chord bisects it.
• If two chords of a circle are congruent, they will be equidistant from the centre.
• Two chords of a circle which are equidistant from the centre are congruent.
• Exercise 9.1
• Exercise 9.2
• Chapter 9 MCQ’s
• Miscellaneous Exercise

Prove the following theorems along with corollaries and apply them to solve appropriate problems.

• If a line is drawn perpendicular to a radial segment of a circle at its outer end point, it is tangent to the circle at that point.
• The tangent to a circle and the radial segment joining the point of contact and the centre are perpendicular to each other.
• The two tangents drawn to a circle from a point outside it are equal in length.
• If two circles touch externally or internally, the distance between their centres is respectively equal to the sum or difference of their radii.
• Exercise 10.1
• Exercise 10.2
• Exercise 10.3
• Miscellaneous Exercise

• If two arcs of a circle (or of congruent circles) are congruent, then the corresponding chords are equal.
• If two chords of a circle (or of congruent circles) are equal, then their corresponding arcs (minor, major or semi-circular) are congruent.
• Equal chords of a circle (or of congruent circles) subtend equal angles at the centre (at the corresponding centre).
• If the angles subtended by two chords of a circle (or congruent circles) at the centre (corresponding centre) are equal, the chords are equal.
• Exercise 11.1
• Chapter 11 MCQ’s
• Miscellaneous Exercise

• The measure of a central angle of a minor arc of a circle is double that of the angle subtended by the corresponding major arc.
• Any two angles in the same segment of a circle are equal.
• The circle angle
• In a semi-circle is a right angle,
• In a segment greater than a semi-circle is less than a right angle,
• In a segment less than a semi-circle is greater than a right angle.
• The opposite angles of any quadrilateral inscribed in a circle are supplementary.
• Exercise 12.1
• Chapter 12 MCQ’s
• Miscellaneous Exercise

• Locate the centre of a given circle.
• Draw a circle passing through three given non-collinear points.
• Complete the circle when a part of its circumference is given,
  • By finding the centre,
  • Without finding the centre.
• Circumscribe a circle about a given triangle.
• Inscribe a circle in a given triangle.
• Escribe a circle in a given triangle.
• Circumscribe an equilateral triangle about a given circle.
• Inscribe an equilateral triangle in a given circle.
• Circumscribe a square about a given circle.
• Inscribe a square in a given circle.
• Circumscribe a regular hexagon about a given circle.
• Inscribe a regular hexagon in a given circle.
• Draw a tangent to a given arc, without using the centre, through a given
• Point p when p is the middle point of the arc, p is at the end o and aand outside the arc.
• Draw a tangent to a given circle from a point P when P is on the circumference and when p is outside the circle.
• Draw two tangents to a circle meeting each other at a given angle.
• Draw direct common tangent or external tangents to two equal circles and draw transverse common tangents or internal tangents to two equal circles.
• Draw direct common tangents or external tangents to two unequal circles and draw transverse common tangents or internal tangents to two unequal circles.
• Draw a tangent to two unequal touching circles and two unequal intersecting circles.
• Draw a circle which touches
• Both the arms of a given a.
• Two converging lines and passes through a given point between them.
• Three converging lines.
• Exercise 13.1
• Exercise13.2
• Chapter 13 MCQ’s